アプリケーション例

ポリシリコンの結晶性評価

背景

アモルファスシリコン（a-Si）は、比較的簡単な加工でトランジスタを作成でき、太陽電池や液晶デバイスなど単結晶シリコン（c-Si）には無い新しい応用分野を切り開きました。
a-Siは加工処理が容易な反面、電子移動度が低いため、トランジスタとしての性能が不十分です。そのため、 a-Siからポリシリコン（p-Si）への置き換えが進んでいます。
p-Siとは、a-Siとc-Siとの中間に相当する存在で、異なる方位を有する単結晶の粒からなっています。p-Siは粒と粒の境界部分（結晶粒界）で、電子が散乱されてしまい、c-Siと比べれば、電子移動度は低いものの、無定形なa-Siと比べれば電子移動度は遥かに大きくなります。
この電子移動度を改善するには、p-Siの結晶性を改善する（つまり単結晶の粒を大きくすること）が必要になってきます。p-Siの結晶性改善としては、アニーリングが用いられ、特に短時間でスポット加工ができ他の部品への影響が少ないレーザーアニーリングがよく用いられています。
一方で、結晶性改善とともに、そのばらつきの管理も必要とされ、個々の結晶性の管理やアニーリング時にその場でフィードバックできることが求められてきています。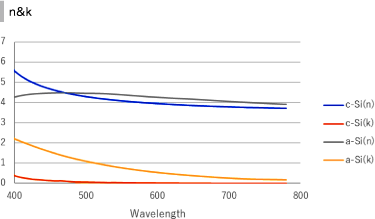

n&k

結晶性と屈折率

c-Siとa-Siでは結晶性が全く異なるため、電気的・光学的性質も異なります。
右のグラフは、c-Siとa-Siの屈折率を示したものです。
p-Siは、その結晶性に応じて、c-Siとa-Siの中間をとります。
結晶性が0％ならa-Siになり、結晶性が100%ならc-Siとなります。
これは、p-Siはc-Siとa-Siの合成物として近似可能なことを表します。このような理論モデルとして、有効媒質近似（EMA）がよく用いられています。

測定例

SiO2膜 p-Si膜 SiO2膜 メタル電極

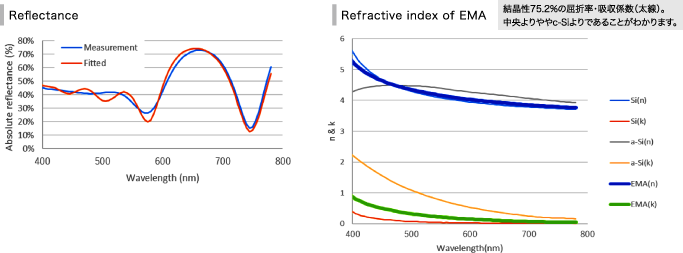
右図のような構造のp-Si膜の結晶性を評価します。
未知パラメータとしては、p-Si膜の結晶性に加え、p-Si膜の膜厚、p-Si膜の上下にあるSiO2膜の膜厚の４個とします。
左下の青線が測定反射率であり、赤線が未知パラメータをFittingしたときの計算波形です。最終的に各パラメータは以下の値が得られます。

  • 結晶性 75.2%
  • p-Si膜厚 188.4nm
  • 下層酸化膜 膜厚 148.6nm
  • 上層酸化膜 膜厚 2.5nm

Reflectance / Refractive index of EMA 結晶性75.2％の屈折率・吸収係数（太線）。中央よりややc-Siよりであることがわかります。

ポーラス膜の密度評価

背景

Low-k材料とはLSI配線を支える層間絶縁材料として使われる誘電率の低い絶縁材料を指します。
誘電率が低い層間絶縁材料を用いると、配線間容量を下げることができ、高速、低消費電力のLSIを実現できます。
従来から使われてきた層間絶縁材料は、SiO2であり、比誘電率は4.2～4.0程度です。
比誘電率を下げるために、空気を含んだポーラス（多孔性）な材料を使います。
一方、ナノポーラス構造では、機械強度や信頼性低下の問題があり、その生産工程での管理が必要とされています。

Low-K膜のモデル化と解析

Low-k膜（≒SiO2+空気） Si基盤

Low-k膜は、SiO2膜と空気（n=1）との混合材料とみなすことができ、その混合比から、
密度、屈折率を見積もることができます。

十分な膜厚があれば、混合比（密度）と膜厚を分離して測定することができます。
左下のグラフは、膜厚100nm、密度50%のLow-k膜に対し膜厚を変化させた分光反射特性です。また、右下のグラフは膜厚100nm、密度50%のLow-k膜に対し密度を変化させたものです。
波形の変化方向が異なるため、膜厚と密度の分離測定が可能であることがわかります。また、それぞれの信号変化量から、nm以下の膜厚分解能と1%以下の密度分解能があることがわかります。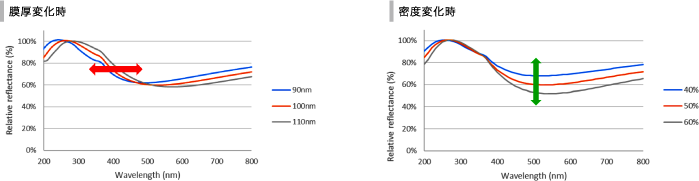

膜厚変化時 密度変化時

ナノメートルオーダーの線幅計測

背景

半導体製造でのリソグラフィ工程では、ナノスケールの回路パターンの限界寸法（CD）計測を行うことが必須となっており、測長SEMやAFMが用いられてきました。近年、特に生産現場においては、光散乱を用いてCDを計測するOCD（Optical Critical Dimension）が台頭しつつあります。これは、スキャトロメトリ（Scatterometory:光波散乱計測）とも呼ばれています。
このOCDは、高スループットで微小スポットを有する分光エリプソメータと、RCWA（厳密結合波理論）を用いパラメータフィッティングを高速で行う演算装置から構成され、高度に特化されています。
ここでは、EMAを用い、簡単に線幅を計測する手法について説明します。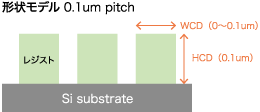

形状モデル 0.1um pitch

線幅測定モデルとRCWA法との相関

右図のような微小線幅も、同様にEMAを用いて近似可能です。
レジスト層は、レジストと空気の混合体として近似でき、その密度が線幅に比例します。
下のグラフは、実際の線幅に対するEMAで求めた密度をプロットしたものであり、線形関係にあることがわかります。この場合も、密度と膜厚を同時に測定することが可能であることがわかります。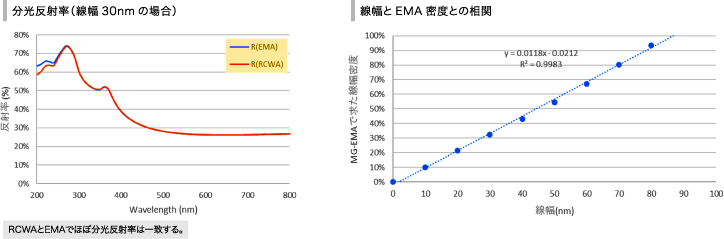

分光反射率（縦線30nmの場合） 線幅とEMA密度との相関

複雑な多層膜構造の評価

以下のようなパターン形状の場合、反射スペクトルから各層の膜厚、エッチング深さを同時に求めることができます。
また、この考え方でMEMS構造やトレンチ深さを求めることも原理的には可能です。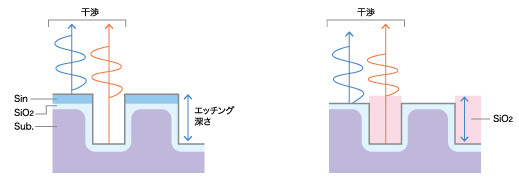

なお、寸法と配置状態によって適用する物理モデルは以下のように異なります。

① 有効媒質（EMA）理論
② Fresnel 多層膜の相互干渉理論
③ 厳密結合波（RCWA又はFMM）理論
　 （断面経常をフーリエ近似を用い、Maxwll方程式を厳密に解く手法。繰り返し構造が前提）

標準アプリケーション でのユーザー様でのレシピ作成は①のみ可能となっております。
②および③につきましては、測定対象毎にカスタムアプリでの対応となります。
特に③においては計算負荷が大きいため、予め計算済みのスペクトルのデータベースを作成しておき、測定時には、それを参照する手法を採用しています。実際の適用可能性については、個別にご相談に応じさせて頂きます。